L'infini
2015-05-21
Salut Ruben !
Je t'envoie la preuve pour convaincre ton père. Je me suis personnellement rendu à l'infini (il se trouve au Havre) et j'ai vérifié que les parallèles s'y joignent.
La photo montre qu'il y a même des flèches qui t'indiquent la direction par où t'es venu et par où tu dois revenir, car quand c'est à l'infini, on ne connaît pas.
Quelques centaines de mètres plus loin il y avait un autre infini, un raté cette fois-ci, où les parallèles n'ont pas réussi à se joindre : on voit que, franchement, c'est n'importe quoi.
T'imagines ce que cela donnerait comme point de fuite dans un tableau avec une perspective ? Ce qui prouve que les parallèles doivent se joindre, sinon c'est le bordel !
Voilà.
A+
Octave






2015-08-20
Salut Octave,
Si deux droites parallèles se rejoignent à l'infini et si elles se rejoignent au Havre, alors c'est que le Havre est à l'infini. Ou alors qu'il y a plusieurs infinis. Ce qui ne me gêne pas, mais en l'occurrence le compactifié d'Alexandrov et son unicité ont du plomb dans l'aile. C'est embêtant. Je me souviens être passé au Havre, c'est pas mal, mais c'est pas l'infini. Houston, on a un problème...
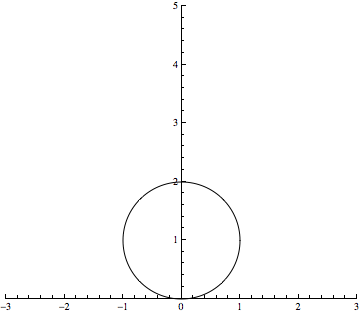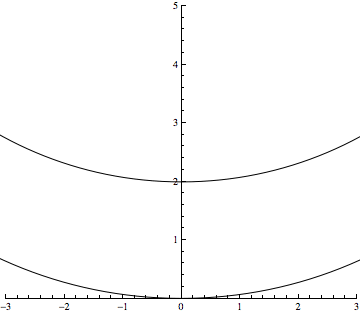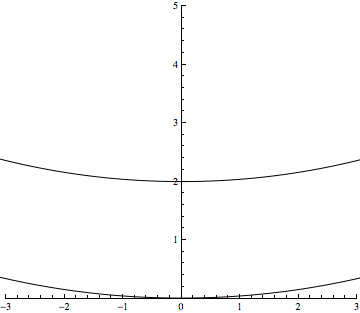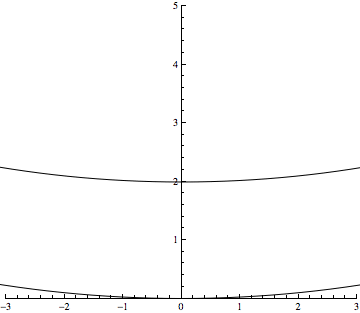
Entre temps j'ai trouvé une autre façon de visualiser la chose. Il s'agit de prendre deux cercles se coupant en un point et de les étirer, à l'infini ! Une animation est en pièce-jointe.
À plus tard !
2015-09-11
Cher Ruben, tu as probablement raison : celui qui est au Havre ne doit pas être le vrai infini. Le vrai infini se trouve sûrement beaucoup plus loin, au moins à 500 km.
Pour ce qui est de ton GIF, en y réfléchissant avec mon cerveau à moi : puisqu’il "n’est pas possible" (= contraire à notre intuition) que deux droites parallèles se rejoignent au même point simultanément par leurs extrèmités opposées, alors les deux cercles, même infiniment grands, doivent garder leurs propriétés et toujours rester des cercles. Leurs arcs tendent vers le parallélisme uniquement localement, sans jamais devenir parallèles, puisqu’il ne s’agit pas de droites. Dans un tel plan conforme à notre expérience, mais étiré avec tout ce qu'il contient à l’infini dans ses deux dimensions, donc infiniment vaste, de tels cercles devraient se confondre quelque soit leur différence de rayon.
Mais peut-être que la première prémisse est fausse et il existe des parallèles se rejoignant en un seul point à l’infini par leurs deux bouts. Ça, ce serait possible dans un espace infini, courbe et fermé dont ces droites feraient en quelque sorte le tour. L’intersection se trouverait chaque fois à l’opposé de l’observateur. Les propriétés qu’ont les cercles sur un plan localement seraient en fait les propriétés de cet espace en même temps fermé et infini (j’ai lu que ça existe, sans comprendre comment, sauf de la sorte, à l’instant).
Donc : soit on a des cercles qui restent des cercles dans un espace plat, soit on a des droites parallèles dans un espace courbe et fermé. Ton .gif est censé de prouver que les parallèles se rejoignent à l’infini même dans un espace plat ? Pas sûr que j’ai compris où tu voulais en venir. J’avoue que les infinis dépassent largement mon cerveau local. Un mathématicien, à l’aise avec les symboles et capable de généralisations, ne s’empêtre pas dans les exemples et peut raisonner à grande échelle, de façon abstraite, à l'abri des intuitions trompeuses. Mais même comme ça, en réfléchissant avec les moyens du bord, on aura au moins compris que l'on ne peut pas raisonner sur l'infini géométrique sans prendre en considération la topologie de l'espace considéré. Finalement, ce sont nos prémisses, devenues axiomes, qui définissent les propriétés topologiques de cet espace. Donc, pour réfléchir sur tes cercles, il nous manque quelque chose. S'il y a un problème, alors son énoncé est incomplet.
En attendant l'élucidation définitive du mystère de l'infini, je te soumets aux fins d’étude un tableau digne d’une thèse concernant un tout autre sujet, voir PJ.
O.